【强化学习算法 14】GPS_恒悦-恒悦平台-注册登录商务站

【强化学习算法 14】GPS

发布：2024-04-07 23:28:47 浏览：次

这里的GPS不是用来导航的GPS，其全称是Guided Policy Search，是一种局域的model-based RL算法，各种版本基本上都是Levine大神搞出来的。

【Importance-sampled GPS】Levine, Sergey, and Vladlen Koltun. "Guided policy search." International Conference on Machine Learning. 2013.

【Variational GPS】Levine, Sergey, and Vladlen Koltun. "Variational policy search via trajectory optimization." Advances in Neural Information Processing Systems. 2013.

【Constraint GPS】Levine, Sergey, and Vladlen Koltun. "Learning complex neural network policies with trajectory optimization."International Conference on Machine Learning. 2014.

【Unknown Dynamics GPS】Levine, Sergey, and Pieter Abbeel. "Learning neural network policies with guided policy search under unknown dynamics."Advances in Neural Information Processing Systems. 2014.

这里有好多版本的，暂时这里只讲第三篇工作。

这里讲了一种model-based的算法，主要思路是先找一条state-action的路径，然后交替地1）优化路径，使得该路径既离现有的控制策略不远，又能够最小化cost；2）优化策略，使得策略离被优化过的路径更近。通过这样trajectory optimization + policy search的方式在bipedal push recovery和walking on uneven terrain问题上取得了较好的实验结果。

continuous state space、continuous action space、model-based with known model dynamics

1. 定义优化问题

首先从一个类似SQL算法的优化目标开始

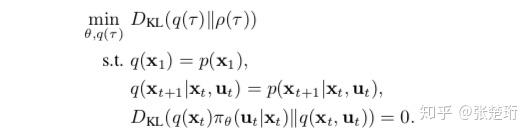
首先先明确一下轨迹 $\ au$ 是状态 $x$ 和控制 $u$ 交替的一个序列。其中 $\\rho(\ au) \\propto \\exp (- l (\ au))$ 是最优轨迹分布，注意到当cost幅值比较大的时候这个最优轨迹更趋近于确定性的轨迹。通过约束，轨迹分布 $q(\ au)$ 就是参数控制的策略 $\\pi_\ heta$ 下形成的轨迹。之所以不直接对最优轨迹 $\\rho(\ au)$ 优化策略，而是要经过中间的 $q(\ au)$ ，是由于在提供了环境模型的情况下，轨迹更容易被优化。

2. dual gradient descent求解

接下来使用dual gradient descent方法来求解上述优化问题，得到算法的大框架

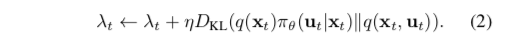
关于dual gradient descent方法可以参考这篇帖子：Dual Gradient Descent

这个主算法里面的第3行是在固定 $\\pi_\ heta$ 和 $\\lambda$ 的情况下优化轨迹 $q(\ au)$ ，第4行是在固定 $q(\ au)$ 和 $\\lambda$ 的情况下优化策略 $\\pi_\ heta$ ，下面分别介绍如何进行这两步操作。

3. 轨迹优化

假定轨迹 $q(\ au)$ 是根据线性策略 $q(u_t|x_t)\\sim \\mathcal{N}(K_t x_t +k_t, A_t)$ 和线性化的动力学 $q(x_{t+1}|x_t, u_t) \\sim \\mathcal{N}(f_{xt}x_t+f_{ut}u_t, F_t)$ 得到的，其整个轨迹上都是高斯分布，令该轨迹分布的均值为 $\\hat{\ au}=(\\hat{x}_{1:T},\\hat{u}_{1:T})$ 。说明：用 $\ au_t=\\left[\\begin{aligned}x_t \\\\ u_t \\end{aligned}\\right]$ 表示拼起来的向量；下标都表示求导；为了和文中一致下标 $xut$ 表示对 $\ au_t$ 的求导；有 hat 上标的表示原来的轨迹，没有 hat 上标的表示相对于原来轨迹的扰动（即小量）。

轨迹是由哪些量描述的呢？我们这里说的轨迹是一个轨迹的概率分布，它是一个高斯型的分布，因此决定它的除了均值 $\\hat{\ au}_t$ 之外，还有 $\ au_t$ 的协方差矩阵

其中 $S_t=Cov[x_t]$ 为定义，其他元素容易求出。

后面的过程比较复杂，我们先要明确一下要我们要干嘛。我们的目标是把问题化为LQG问题（动力学线性、损失函数二次型），然后利用类似iLQG的最优控制公式求解当前轨迹 $q(\ au)$ 附近的更好的新轨迹 $q_{new}(\ au)$ 。我们这里说的轨迹是由如下参数构成的 $q(\ au)=\\{\\hat{\ au}, \\Sigma (S, A, K)\\}$ 。

首先对轨迹进行优化的时候认为 $\\pi_\ heta$ 和 $\\lambda$ 是固定的，我们可以把损失函数写成只与轨迹有关的形式，通过一些计算之后能够得到（注意，这里省略了对于时间 t 的求和）

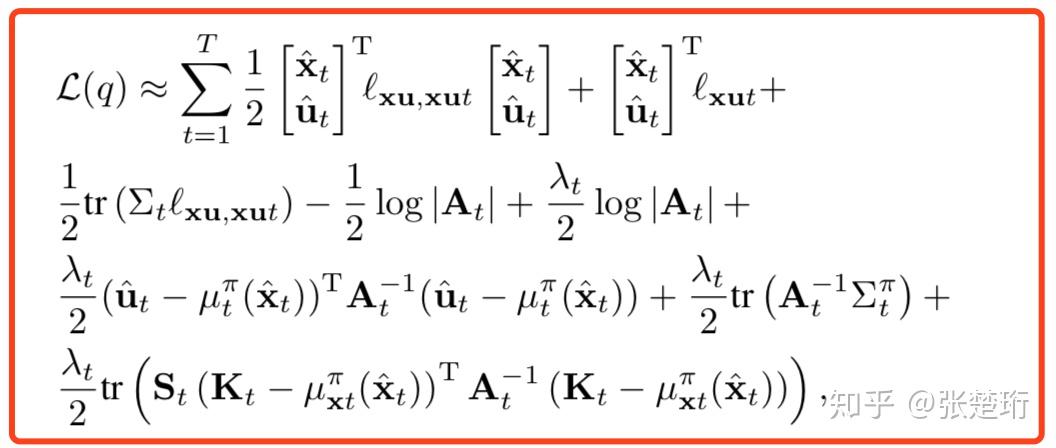
类比 iLQG 算法里面的损失函数 $\\mathcal{L}\\sim (g + Gx)u + \\dfrac{1}{2}u^T H u$ ，有最优控制 $u_t=k_t + K_t x_t$ 。我们的思路就是针对上面损失函数把相应的项找出来，其方法也很简单就是把上面的损失函数对控制 $u_t$ 求导，可以得到

但是当你求的时候会发现，求出来的形式跟文章一样，但是你式子里面出现单状态损失函数 $\\mathcal{l}$ （这个说法不是规范的说法，为了方便叙述我自己编的）的时候，文章里面都写的是 $Q$ 。为什么这样呢？因为当你改变了某一处控制函数的时候，它后面相应的轨迹也都发生了改变，因此当某一处控制函数的改变导致了单状态损失函数的时候，应该连带上它对于后续轨迹上损失函数的改变，即用下面的 $Q$ 来替代即可

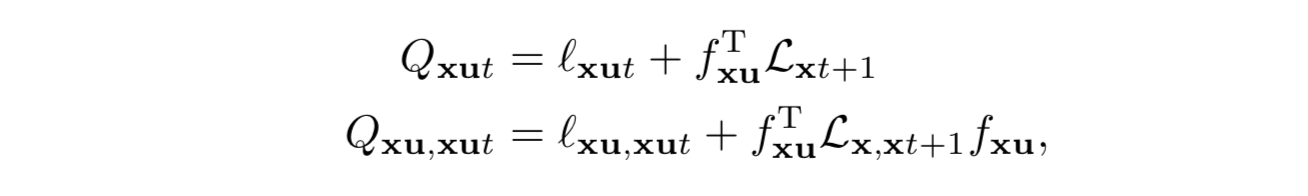
接下来，比对 iLQG 的算法公式能够得到新的最优控制扰动

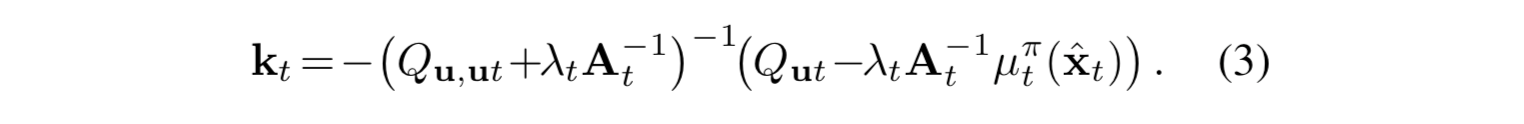
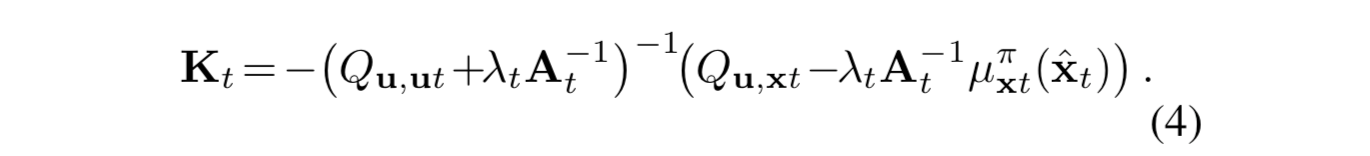
注意到，其中 Q 的计算是包含损失函数在后一步上的导数的，因此该过程需要通过逆序的动态规划来求解。计算 Q 会用到的损失函数计算公式如下。

由此我们能够确定新的轨迹的均值 $\\hat{\ au}_{new}=\\hat{\ au}+ \ au$ ，而该新轨迹的协方差矩阵 $\\Sigma_{new}$ 也需要被确定，观察上面关于协方差矩阵的定义，如果我们求出了 $S_t$ 、 $A_t$ 和 $K_t$ ，就可以确定轨迹的协方差矩阵了。

知道新轨迹的均值之后怎么求出相应的 $S_t$ 、 $A_t$ 和 $K_t$ 呢？自然想到的就是对损失函数相对于要求的这些量求导，并且令导数为零。同样，为了避免轨迹协方差变化对于后续轨迹产生的影响，我们需要把单状态损失函数替换为

求导可得

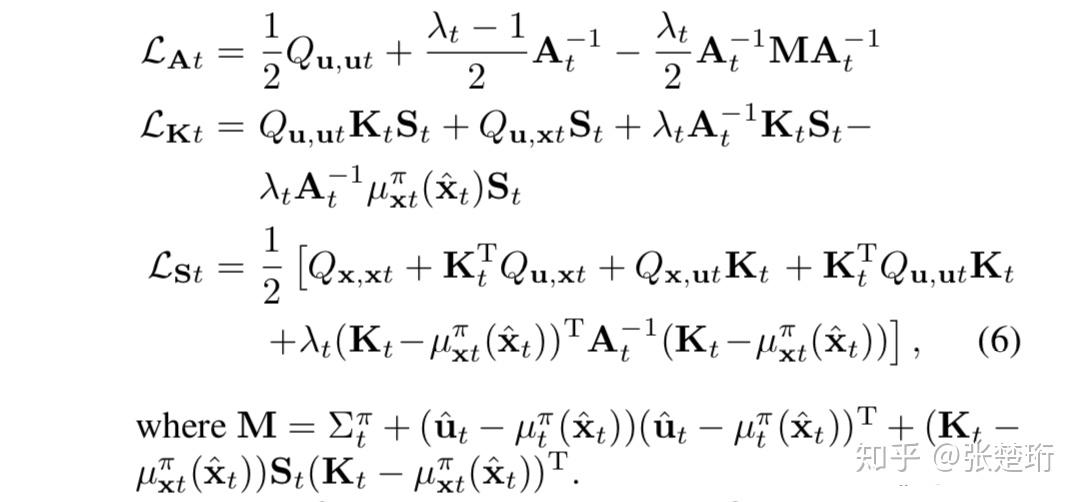
零导数为零，可得

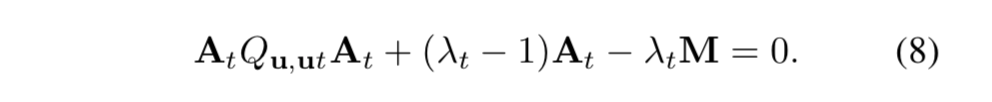
由于 $S_t$ 、 $A_t$ 和 $K_t$ 相互依赖，因此我们需要迭代多次直到它们数值收敛。

4. 策略优化

有了更优的轨迹之后，我们接下来把轨迹固定，来优化相应的策略，这一步的优化相对来讲就比较直接了：写出关于损失函数关于策略参数 $\ heta$ 的表示，然后使用梯度方法做优化即可，比如SGD或者LBFGS。

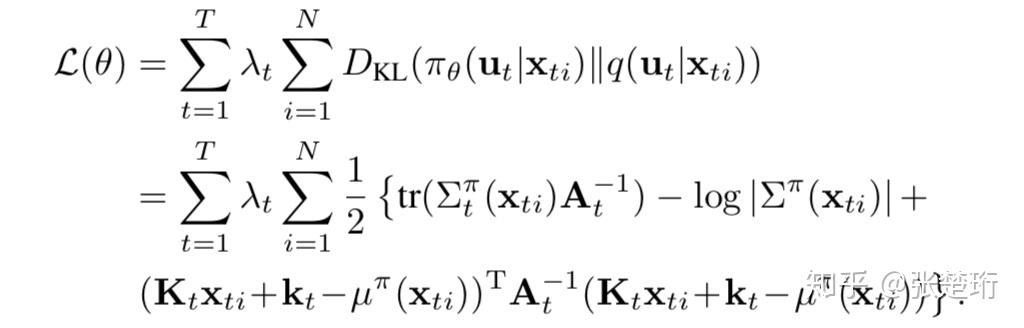
其中算法1是主要的算法，算法2是其中第3行的具体算法。其中值得说明的是，第7-10行在最优开环控制上面缩小，以找到确定能改善损失函数的开环控制，其原因是由于环境是非线性的，而我们在局域假设了线性，因此如果开环控制变化的太多会导致假设不成立，形成的损失函数甚至不降反升。另外，第10行的大于符号应该是写错了，应该是小于符号，这里希望做的是最小化损失函数。

从绿框公式到红框公式的推导？

$\\begin{aligned}D_{KL}(q(\ au) || \\rho(\ au)) &=\\sum_{t=1}^T D_{KL}(q(x_t, u_t) || \\rho(x_t, u_t)) \\\\ &=\\sum_{t=1}^T\\int q(x_t, u_t)[\\log q(x_t, u_t) - \\log(\\rho(x_t, u_t))]dx_t du_t \\\\ &=\\sum_{t=1}^T \\mathcal{H}(q(x_t, u_t)) + \\mathbb{E}_{q(x_t, u_t)}[l(x_t, u_t)]\\end{aligned}$

注意每一步的熵函数其实并不独立，后面的会依赖前面的，所以上面这样写其实不规范，不过我们在运算的过程中记住这一点就好了，同时，高斯分布的熵函数为

有

$\\begin{aligned}\\mathcal{H}(q(x_t, u_t)) &=\\int q(x_t, u_t) \\log q(x_t, u_t) dx_t du_t \\\\ &=\\int q(x_t, u_t) \\log q(x_t | x_{t-1}, u_{t-1}) dx_t du_t + \\int q(x_t, u_t) \\log q(u_t| x_t) dx_t du_t \\\\ &=\\int q(x_t) \\log q(x_t | x_{t-1}, u_{t-1}) dx_t + \\int q(u_t) \\log q(u_t| x_t) du_t \\\\ &=-1 -\\log 2\\pi - \\dfrac{1}{2}|A_t| - \\dfrac{1}{2}|F_t| \\\\ & \\sim - \\dfrac{1}{2}|A_t| \\end{aligned}$

其中随后一步是因为，求导的损失函数是要对于轨迹参数求导的，无关的常数项就可以不写了，有

注意到 $\\mathbb{E}_q[\ au_t]=\\hat{\ au}_t$ ，有

$\\begin{aligned}\\mathbb{E_{q(x_t, u_t)}}[l(x_t, u_t)]&=\\mathbb{E_{q(x_t, u_t)}}[l(0, 0) + l_{xut}^T \ au_t + \\frac{1}{2}\ au_t^T l_{xuxut}\ au_t ]\\\\ &=l(0, 0) + l_{xut}^T \\hat{\ au}_t + \\frac{1}{2}\\mathbb{E_{q(x_t, u_t)}}[(\ au_t - \\hat{\ au}_t + \\hat{\ au}_t)^T l_{xuxut}(\ au_t - \\hat{\ au}_t + \\hat{\ au}_t)]\\\\ &=l(0, 0) + l_{xut}^T \\hat{\ au}_t +\\frac{1}{2}\\mathbb{E_{q(x_t, u_t)}}[(\ au_t - \\hat{\ au}_t)^T l_{xuxut}(\ au_t - \\hat{\ au}_t)]+\\frac{1}{2}\\mathbb{E_{q(x_t, u_t)}}[(\ au_t - \\hat{\ au}_t)^T l_{xuxut}\\hat{\ au}_t]\\\\ & \\quad + \\frac{1}{2}\\mathbb{E_{q(x_t, u_t)}}[\\hat{\ au}_t^T l_{xuxut}(\ au_t - \\hat{\ au}_t)]+ \\frac{1}{2}\\mathbb{E_{q(x_t, u_t)}}[\\hat{\ au}_t^T l_{xuxut}\\hat{\ au}_t]\\\\ &=l(0, 0) + l_{xut}^T \\hat{\ au}_t + \\frac{1}{2}tr(\\Sigma_t l_{xuxut}) + 0 + 0 + \\frac{1}{2}\\hat{\ au}_t^T l_{xuxut}\\hat{\ au}_t\\\\ & \\sim l_{xut}^T \\hat{\ au}_t + \\frac{1}{2}tr(\\Sigma_t l_{xuxut}) + \\frac{1}{2}\\hat{\ au}_t^T l_{xuxut}\\hat{\ au}_t\\\\ \\end{ali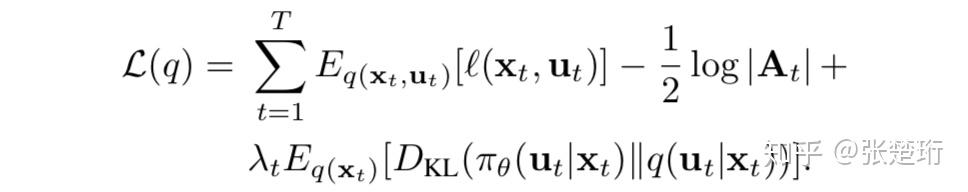gned}$

其中最后一个等号的成立可以参看这个课件的第六页。

同时注意到高斯函数的交叉熵

有

$\\begin{aligned}& \\mathbb{E}_{q(x_t)}[D_{KL}(\\pi_\ heta (u_t | x_t) || q(u_t | x_t))]\\\\=& \\mathbb{E}_{q(x_t)}[\\int \\pi_\ heta (u_t | x_t) \\log \\pi_\ heta (u_t | x_t) du_t]- \\mathbb{E}_{q(x_t)}[\\int \\pi_\ heta (u_t | x_t) \\log q(u_t | x_t) du_t]\\\\ \\sim & 0 + \\frac{1}{2}tr(A_t^{-1}\\Sigma^\\pi_t) + \\frac{1}{2}\\log |A_t| + \\frac{1}{2}\\mathbb{E}_{q(x_t)}[(u_t - \\mu^\\pi_t(x_t))^T A_t^{-1}(u_t - \\mu^\\pi_t(x_t))]\\\\=& \\frac{1}{2}tr(A_t^{-1}\\Sigma^\\pi_t) + \\frac{1}{2}\\log |A_t| + tr(S_t (K_t - \\mu_{xt}^\\pi)^T A_t^{-1}(K_t - \\mu_{xt}^\\pi)) + (\\hat{u}_t - \\mu_\\pi(\\hat{x}_t))^T A_t^{-1}(\\hat{u}_t - \\mu_\\pi(\\hat{x}_t)) \\end{aligned}$

其中约等于符号是因为前一项是完全关于策略的，与我们这里要优化的轨迹无关，因此不理会这一项，其中比较复杂的最后一项细写下来是

$\\begin{aligned}& \\mathbb{E}_{q(x_t)}[(K_t x_t - \\mu^\\pi_t(x_t))^T A_t^{-1}(K_t x_t - \\mu^\\pi_t(x_t))]\\\\=& \\mathbb{E}_{q(x_t)}[(K_t x_t - K_t \\hat{x}_t + \\hat{u}_t - \\mu_\\pi(\\hat{x}_t) + \\mu_\\pi(\\hat{x}_t) -\\mu_\\pi(x_t))^T A_t^{-1}(\\cdots)]\\\\=& \\mathbb{E}_{q(x_t)}[( (K_t - \\mu_{xt}^\\pi) (x_t - \\hat{x}_t) + (\\hat{u}_t - \\mu_\\pi(\\hat{x}_t)) )^T A_t^{-1}(\\cdots)]\\\\=& \\mathbb{E}_{q(x_t)}[( (K_t - \\mu_{xt}^\\pi) (x_t - \\hat{x}_t) )^T A_t^{-1}(\\cdots)]+ 0 + 0 + \\mathbb{E}_{q(x_t)}[(\\hat{u}_t - \\mu_\\pi(\\hat{x}_t)) ^T A_t^{-1}(\\cdots)]\\\\=& tr(S_t (K_t - \\mu_{xt}^\\pi)^T A_t^{-1}(K_t - \\mu_{xt}^\\pi)) + (\\hat{u}_t - \\mu_\\pi(\\hat{x}_t))^T A_t^{-1}(\\hat{u}_t - \\mu_\\pi(\\hat{x}_t)) \\end{aligned}$

其中轨迹的控制和策略的控制都有直流项的，但是由于后面求协方差并不影响，为了简便，这里就不写直流项了。

最后拼起来有

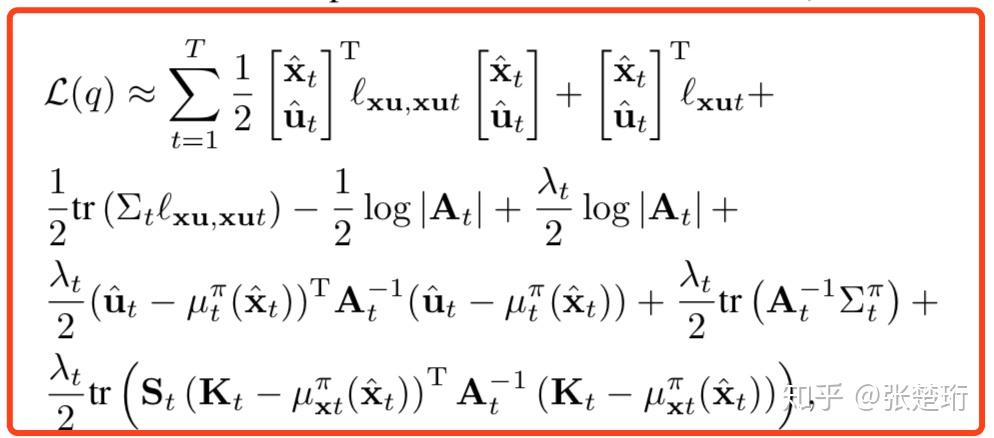
推导过程参考了【强化学习大讲坛】强化学习进阶第九讲引导策略搜索。